The bubble sort algorithm in Python is the topic of this lesson. Bubble sort is a very simple sorting algorithm to implement, but we must say that it is also inefficient.
In fact, the bubble sort is mainly used in the didactic field to teach the logic and basics of programming.
How bubble sort work
The elements close to each other are compared, bringing the largest element to the last position during the first “pass” (by performing n-1 comparisons), then the second maximum to the penultimate position and so on until the array is sorted.
Then at each step, the next largest value is inserted in the list in the right place.
The complexity of the algorithm is O (n2), both in the worst case and in the best case.
Implementation of the bubble sort algorithm in Python
I implement the bubble sort solution in Python in a different way than in other programming languages. This is because a temporary support variable is not needed for variable exchange in Python.
Banner Pubblicitario
In this guide I deal with the topic of the exchange of variables. How to exchange the value of variables
Therefore this operation will not be necessary:
temp = a;
a = b;
b = temp;
But simply write:
a,b = b,a
This procedure, called concurrent assignment, allows me to streamline the bubble sort algorithm in Python.
def bubbleSort(array):
for j in range(0, len(array)-1):
for i in range(0, len(array)-1):
if array[i]>array[i+1]:
array[i], array[i+1] = array[i+1], array[i]
array_numbers = [54,26,93,17,77,31,44,55,20]
bubbleSort(array_numbers)
print(array_numbers)
The algorithm is very simple, based on the comparison of adjacent elements.
But what if the algorithm was ordered? In any case, I should always repeat the external cycle n-1 times. We can then think about making optimizations to the proposed algorithm.
Optimization of the bubble sort algorithm in Python – sorting by exchange with sentinel
We can think of interrupting the outer for loop, with a break, if no swap has been made at the end of the first inner loop. For this purpose we use a support variable called flag, which we initialize to 0. Afterwards, we change the value of this variable if at least one exchange is made in the inner loop. As an alternative to 0 and 1 I can use a Boolean variable.
Banner pubblicitario
Here is the sample code:
def bubbleSort(array):
for j in range(0, len(array)-1):
flag = False
for i in range(0, len(array)-1):
if array[i]>array[i+1]:
array[i], array[i+1] = array[i+1], array[i]
flag = True
if not(flag):
break
array_numbers = [54,26,93,17,77,31,44,55,20]
bubbleSort(array_numbers)
print(array_numbers)
Second optimization of the bubble sort algorithm in Python
We can optimize the bubble sort algorithm by reflecting on the fact that with each increment of j, at least the last j + 1 elements have already been sorted. This is in consideration of the fact that with each iteration, the largest element has been shifted to the right.
So at each iteration we shorten the cycle of comparisons. In fact, at the n-th iteration it is possible to do without touching the last n-1 elements that are now in their final position. Therefore we decrease n by one at each iteration (- -n), in order to decrease by 1, each time, the number of comparisons made.
Here is the complete code of the optimized algorithm:
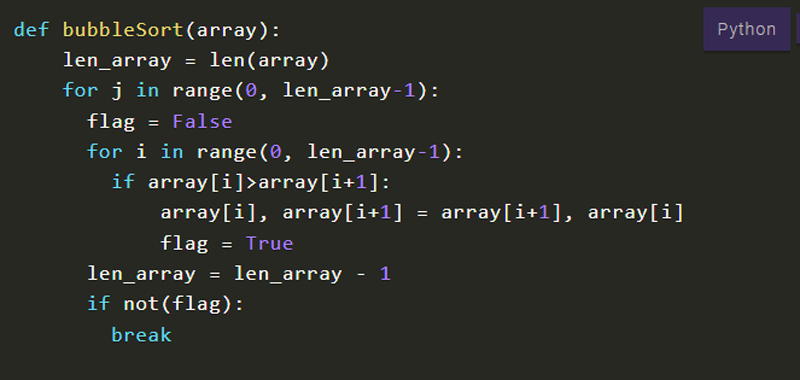
def bubbleSort(array):
len_array = len(array)
for j in range(0, len_array-1):
flag = False
for i in range(0, len_array-1):
if array[i]>array[i+1]:
array[i], array[i+1] = array[i+1], array[i]
flag = True
len_array = len_array - 1
if not(flag):
break
array_numbers = [54,26,93,17,77,31,44,55,20]
bubbleSort(array_numbers)
Third optimization of the bubble sort algorithm in Python
A further optimization to the bubble sort algorithm in Python can be developed in consideration of the fact that the inner loop stops right where the swap took place. Therefore, after each iteration, more elements are in the final position and you can avoid reordering them.
It is necessary to memorize the position (i + 1) of the last exchange carried out in a variable that we will call for example pos. Then we assign the value of pos to the length of the array.
Here is a possible implementation of the optimized algorithm:
def bubbleSort(array):
len_array = len(array)
for j in range(0, len_array-1):
flag = False
for i in range(0, len_array-1):
if array[i]>array[i+1]:
array[i], array[i+1] = array[i+1], array[i]
flag = True
pos = i + 1
if not(flag):
break
else:
len_array = pos
print(i,j)
array_numbers = [54,26,93,17,77,31,44,55,20]
bubbleSort(array_numbers)
print(array_numbers)
Conclusioni
In this lesson I made some implementations of the bubble sort algorithm in Python, trying to optimize an algorithm that is simple to implement, but slow. In the next few lessons I will explain other sorting algorithms.










Commenti recenti