Python Merge Sort

We develop the Python Merge Sort algorithm, one of the most famous sorting algorithms that uses the divide and conquer method, as well as the Quick Sort.

First of all we explain how this algorithm works.

First we divide the list into two sublists and then gradually into even smaller parts. Then we use a recursive function on each sublist and finally we combine the result in order to obtain the solution to the sorting algorithm.

Python Merge Sort – solution

Suppose we have a list of integers:

numbers = [6,12,4,3,7,8]

We indicate the index pointing to the number 6 with p and the index pointing to the number 8 with r.

numbers = [p,…,…, r]

As a first step, therefore, we divide the list in half using another index, for example q:

so we will have numbers_1 = [p,…,…, q] and numbers_2 = [q + 1,…,…, r]

It continues to divide until it can no longer be divided. This condition occurs when the array is empty or there is only one element left (ie 0 elements or 1).

The recursive sorting function is then invoked on each of the two halves. Finally it all comes combine.

In our example we have:

numbers = [6,12,4,3,7,8]

therefore: numbers_1 = [6,12,4,] and numbers_2 = [3,7,8] and so on.

Here, then, is a graphic representation of what happens:

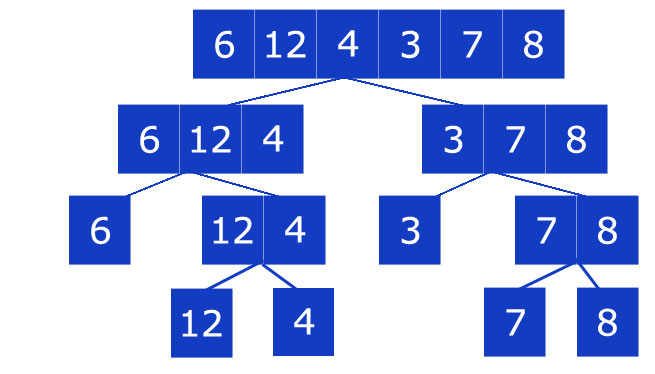
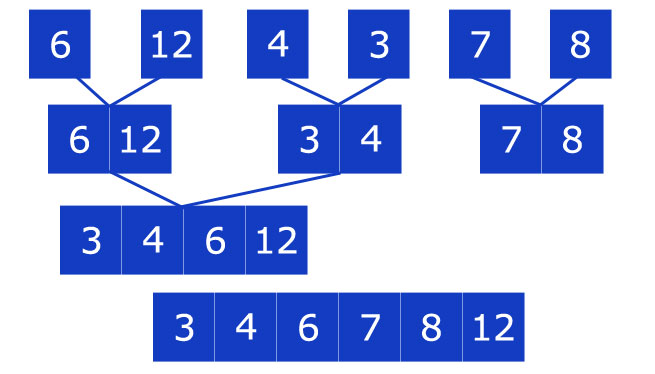
Now that all the elements are divided, let’s use a support list and start sorting.

The second part of the Merge Sort algorithm, therefore, concerns the actual ordering of the elements in an order that can be increasing or decreasing.

We choose an increasing order. We sort and then combine each part of the sublists.

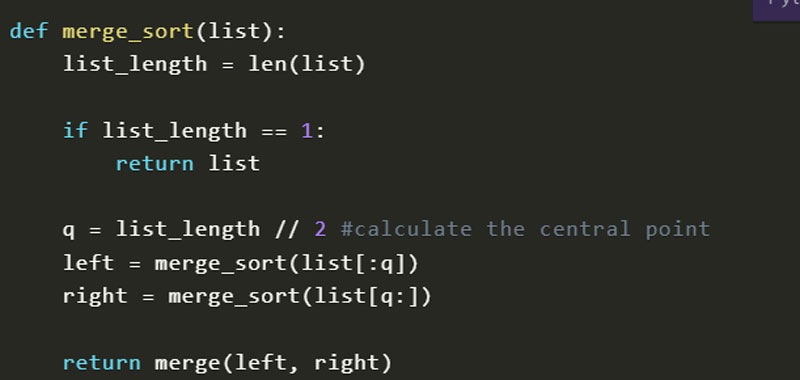
Python Merge Sort – code

Here is therefore a possible solution to the algorithm:



def merge_sort(list):
    list_length = len(list)

    if list_length == 1:
        return list

    q = list_length // 2 #calculate the central point
    left = merge_sort(list[:q]) 
    right = merge_sort(list[q:])

    return merge(left, right)

def merge(left, right):
    ordered = []
    
    while left and right:
        ordered.append((left if left[0] <= right[0] else right).pop(0))
    return ordered + left + right


numbers = [10,5,12,1,9]
print(numbers)
sorted_list = merge_sort(numbers)
print(sorted_list)

Try the code in the compiler below:

Clearly that proposal is a possible solution to the Python Merge Sort algorithm, please implement yours and write it in the comments below.

Prev lesson: Insertion Sort in Python

Next lesson: Quick Sort in Python