Realizziamo un programma in C che, data una matrice quadrata di ordine N, determini la somma degli elementi della diagonale principale di una matrice.
Definizione di diagonale principale di una matrice
La diagonale principale di una matrice quadrata è la diagonale che va dall’angolo in alto a sinistra a quello in basso a destra.
La diagonale secondaria di una matrice quadrata è la diagonale che va dall’angolo in alto a destra a quello in basso a sinistra.
Nella figura sotto ho evidenziato in rosso la diagonale principale e in verde quella secondaria.
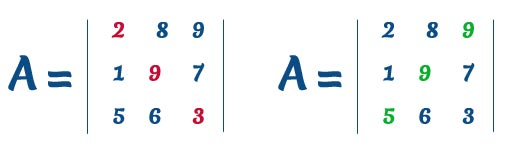
Procedimento
Vogliamo dunque costruire un algoritmo che, data una matrice quadrata di ordine N, determini la somma degli elementi della diagonale principale di una matrice.
Innanzitutto prendiamo in input una matrice quadrata di ordine N, inseriamo i dati nella matrice e facciamo queste considerazioni.
Banner Pubblicitario
La diagonale principale di una matrice 3 x 3 è data dagli elementi a(0,0) , a(1,1) e a(2,2).
Mentre la diagonale principale di una matrice 4 x 4 è data dagli elementi a(0,0) , a(1,1) , a(2,2) e a(3,3). E così via.
Quindi la diagonale principale di una matrice è data dagli elementi il cui indice j è uguale all’indice i.
Pertanto per ottenere la somma, basta semplicemente fare:
for(i=0;i<n;i++)
somma_d += a[i][i];
/*somma_d è la variabile che contiene la somma degli elementi con indice j=i.*/Allo stesso modo ragioniamo per la diagonale secondaria.
Gli elementi della diagonale secondaria di una matrice 3 x 3 sono a(0,2) , a(1,1) e a(2,0).
Mentre se la matrice è 4 x 4 gli elementi della diagonale secondaria sono a(0,3) , a(1,2) , a(2,1) e a(3,0).
Banner pubblicitario
Notiamo, nel caso della matrice 3×3, che l’indice i parte da 0 e arriva a 2 mentre l’indice j parte da 2 e arriva a 0, cioè l’indice i si incrementa mentre l’indice j si decrementa. Così anche nella matrice 4 x4, ecc…
Dunque per queste considerazioni avremo:
for(i=0,j=n-1;i<n;i++,j--)
somma_s += a[i][j];
/*somma_s è la variabile che contiene la somma degli elementi della diagonale secondaria*/Allego tutto il listato
#include<stdio.h>
#define N 100
int main(){
int a[N][N],n,m,i,j,somma_d=0,somma_s=0;
do {
printf("Dammi il numero di righe e colonne: ");
scanf("%d", &n);
} while ((n>N) || (N<1));
printf("\nInseriamo i dati nella matrice \n");
for (i=0;i<n;i++)
for (j=0;j<n;j++) {
printf("Inserisci elemento di riga %d e colonna %d: ", i, j);
scanf("%d", &a[i][j]);
}
printf("\nStampiamo i dati \n");
for (i=0;i<n;i++) {
printf("\n");
for(j=0;j<n;j++)
printf("\t%d", a[i][j]);
}
for(i=0;i<n;i++)
somma_d += a[i][i]; //somma diagonale principale
for(i=0,j=n-1;i<n;i++,j--)
somma_s += a[i][j];*/ //somma diagonale secondaria
printf("la somma della diagonale principale e' %d\n",somma_d);
printf("la somma della diagonale secondaria e' %d\n",somma_s);
}Esempio di calcolo della somma degli elementi che si trovano sopra la diagonale principale.
Adesso ci poniamo il problema di voler calcolare la somma degli elementi che si trovano sopra la diagonale principale, in definitiva gli elementi della sotto-matrice triangolare superiore.
Quindi facciamo nuovamente le nostre considerazioni.
Nel caso di una matrice 3 x 3, gli elementi che si trovano al di sopra la diagonale principale sono a(0,1) , a(0,2) e a(1,2).
Nel caso di una matrice 4 x 4, gli elementi che si trovano al di sopra la diagonale principale sono a(0,1) , a(0,2) , a(0,3) , a(1,2) , a(1,3) e a(2,3).
Uno dei modi per ottenere ciò è usare due cicli.
//somma elementi al di sopra della diagonale principale
for(i=0;i<n-1;i++)
for(j=i+1;j<n;j++)
somma+=a[i][j];Analogamente per sommare gli elementi al di sotto della diagonale principale, ovvero gli elementi della sotto-matrice triangolare inferiore.
//somma elementi al di sotto della diagonale principale
for(j=0;j<n;j++)
for(i=j+1;i<n;i++)
somma2+=a[i][j]; Dunque, allego il listato completo:
#include<stdio.h>
#define N 100
int main(){
int a[N][N],n,m,i,j,somma=0,somma2=0, somma_d=0, somma_s=0;
do {
printf("Dammi il numero di righe e colonne: ");
scanf("%d", &n);
} while ((n>N) || (N<1));
printf("\nInseriamo i dati nella matrice \n");
for (i=0;i<n;i++)
for (j=0;j<n;j++) {
printf("Inserisci elemento di riga %d e colonna %d: ", i, j);
scanf("%d", &a[i][j]);
}
printf("\nStampiamo i dati \n");
for (i=0;i<n;i++) {
printf("\n");
for(j=0;j<n;j++)
printf("\t%d",a[i][j]);
}
for(i=0;i<n;i++)
somma_d += a[i][i]; //somma diagonale principale
for(i=0,j=n-1;i<n;i++,j--)
somma_s += a[i][j]; //somma diagonale secondaria
//somma elementi al di sopra della diagonale principale
for(i=0;i<n-1;i++)
for(j=i+1;j<n;j++)
somma+=a[i][j];
//somma elementi al di sotto della diagonale principale
for(j=0;j<n;j++)
for(i=j+1;i<n;i++)
somma2+=a[i][j];
printf("\nla somma della diagonale principale e' %d\n",somma_d);
printf("la somma della diagonale secondaria e' %d\n",somma_s);
printf("la somma degli elementi sopra diagonale principale e' %d\n",somma);
printf("la somma degli elementi sotto diagonale principale e' %d\n",somma2);
}Se ad esempio volessimo ottenere la somma degli elementi della diagonale che sta sotto quella principale, allora basterebbe sommare gli elementi di posto a[i+1][i].
for(i=0;i<n-1;i++)
somma_d1 += a[i+1][i];Questi sono solo degli esempi di possibili soluzioni agli esercizi proposti. Proponete pure le vostre nei commenti sotto.
Alcuni link utili:
Somma elementi cornice esterna
Somma dei numeri di una matrice
Ricerca elementi in una matrice










Trackback/Pingback