Equazioni di secondo grado in C++, uso di funzioni in C++

In questa lezione risolveremo le equazioni di secondo grado in C++.

Affronteremo questo esercizio per approfondire ancora le funzioni in C++.

Abbiamo già proposto lo stesso esercizio in C, se volete potete seguire il link: equazioni in C.

Equazioni di secondo grado

Un’equazione di secondo grado scritta nella forma canonica è:

ax² + bx + c = 0

Per risolvere questa equazione occorre conoscere i valori dei coefficienti a, b e c.

Dopo occorre trovare il delta o determinante utilizzando questa formula: b * b – 4 * a * c.

Scatena il tuo potenziale con ’50 Algoritmi per imparare C++’, il libro appena lanciato su Amazon che ti guiderà nel mondo della programmazione con passione e precisione!

Acquistalo su Amazon

In base al risultato potremmo trovarci in tre situazioni distinte:

nel caso in cui il determinante è minore di zero, allora non esistono soluzioni reali;

se invece il determinante è uguale a zero, l’equazione ammette due soluzioni reali coincidenti;

infine, se il determinante è maggiore di zero, l’equazione ammette due soluzioni reali distinte.

Inoltre osserviamo che, se il coefficiente a è uguale a zero, non ci troveremmo più di fronte ad un’equazione di secondo grado ma ovviamente di primo grado: bx+c. Dunque non si potrà applicare la formula.

Quando le soluzioni esistono si ottengono con questa formula:

x1 = (-b+sqrt(determinante)) / 2*a

x2 = (-b-sqrt(determinante)) / 2*a

utilizziamo sqrt (dalla libreria cmath) come funzione per il calcolo della radice quadrata.

Strutturiamo il programma scomponendolo in sottoprogrammi:

funzione coefficienti() per prendere in input i coefficienti.

funzione determinante() per il calcolo del determinante.

funzioni soluzioni() per il calcolo delle soluzioni.

funzione equazione_primo() nel caso in cui l’equazione sia di primo grado.

Ecco il listato completo del programma in C++ per il calcolo delle equazioni di secondo grado.

#include <iostream>
#include <cmath> // Per utilizzare la funzione sqrt()

using namespace std;

float a, b, c; // Coefficienti dell'equazione
double x1, x2, d; // Soluzioni e determinante

// Funzione per inserire i coefficienti dell'equazione
void coefficienti() {
    cout << "Coefficient a: ";
    cin >> a;
    cout << "Coefficient b: ";
    cin >> b;
    cout << "Coefficient c: ";
    cin >> c;
}

// Funzione per calcolare il determinante dell'equazione
void determinante() {
    d = b * b - 4 * a * c;
}

// Funzione per calcolare le soluzioni dell'equazione
void soluzioni() {
    if (d < 0)
        cout << "Non ci sono soluzioni reali" << endl;
    else if (d == 0) {
        x1 = (-b) / (2 * a);
        cout << "Due soluzioni reali coincidenti x1 e x2: " << x1;
    } else {
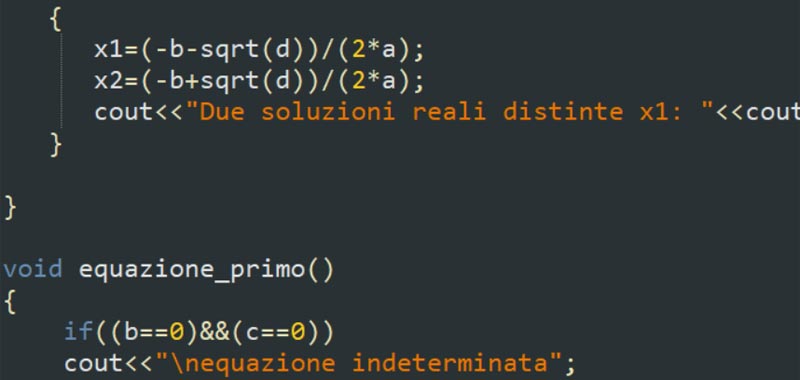
        x1 = (-b - sqrt(d)) / (2 * a);
        x2 = (-b + sqrt(d)) / (2 * a);
        cout << "Due soluzioni reali distinte x1: " << x1 << " e x2: " << x2;
    }
}

// Funzione per risolvere un'equazione di primo grado
void equazione_primo() {
    if ((b == 0) && (c == 0))
        cout << "\nEquazione indeterminata";
    else if (b == 0)
        cout << "\nEquazione impossibile";
    else {
        x1 = -c / b;
        cout << "x: " << x1;
    }
}

int main() {
    coefficienti(); // Inserimento dei coefficienti
    
    if (a == 0)
        equazione_primo(); // Equazione di primo grado
    else {
        determinante(); // Calcolo del determinante
        soluzioni(); // Calcolo delle soluzioni
    }

    return 0;
}

Chiaramente questo è solo un esempio di possibile risoluzione di un’equazione di secondo grado in C++.