In questo articolo affronteremo le potenze con Scratch.
Le potenze si indicano in questo modo:
an dove a è la base ed n è l’esponente.
Le potenze sono delle moltiplicazioni ripetute, quindi an è uguale ad a*a*a…*a eseguito n volte.
Facciamo degli esempi.
23 è uguale a 2*2*2, cioè 2 moltiplicato per se stesso 3 volte.
Banner Pubblicitario
35 è uguale a 3*3*3*3*3, cioè 3 moltiplicato per se stesso 5 volte.
In particolare avremo:
a0 è uguale a 1 se a è diverso da zero.
a0 è non definito se a è uguale a zero (00).
0n con n diverso da zero è uguale a zero.
Algoritmo per calcolare le potenze con Scratch
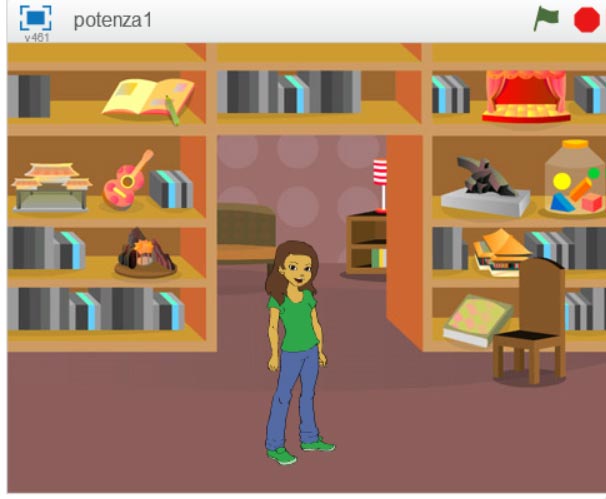
Innanzitutto scegliamo uno sfondo e uno sprite.
Io ho scelto questi:
Banner pubblicitario
Poi creiamo le variabili necessarie, cioè la base, l’esponente e la potenza che è la variabile che conterrà il risultato delle operazioni.

Adesso non ci resta che calcolare l’algoritmo per il calcolo delle potenze con Scratch.
Teniamo conto di quanto detto sopra e quindi consideriamo i casi particolari:
Se la base e l’esponente sono uguali a zero, allora si avrà il messaggio in output: la potenza non è definita.
Se solo la base è uguale a zero, allora la potenza sarà sempre zero.
Invece, se nessuna delle condizioni è verificata passiamo al calcolo della potenza. Come? Con il metodo delle moltiplicazioni ripetute.
Portiamo la variabile potenza uguale a 1 e poi ripetiamo tante volte quanto è l’esponente la moltiplicazione del numero per se stesso.
Facciamo un esempio, prendendo in considerazione 23.
Quindi il ciclo si ripeterà 3 volte e i passaggi saranno questi:
Prima iterazione potenza=potenza *base=1*2=2
Seconda iterazione potenza=potenza*base=2*2=4
Terza iterazione potenza=potenza*base=4*2=8
Infine mi dirà il risultato.
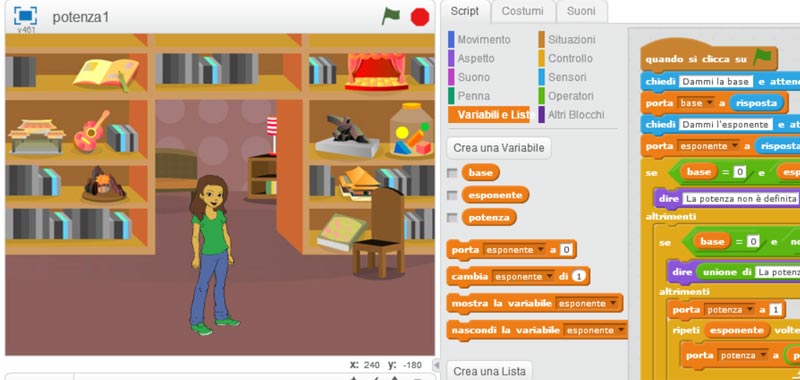
Ecco l’algoritmo completo per il calcolo della potenza con scratch.
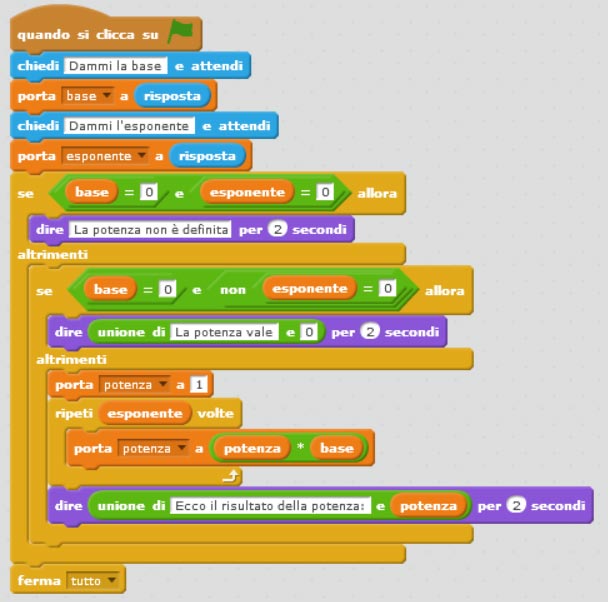
Ma attenzione se l’esponente è negativo?
Algoritmo per calcolare la potenza con Scratch nel caso in cui l’esponente è negativo
Per calcolare questo algoritmo teniamo conto che, se eleviamo a potenza con un numero negativo allora il risultato sarà dato dal reciproco della base con l’esponente cambiato di segno.
Facciamo degli esempi:
2-1 è uguale a 1/2 ovvero 0,5.
2-2 è uguale a 1/4 ovvero 0,25.
Quindi facciamo questa operazione: se l’esponente è negativo lo trasformiamo in positivo. Dopo con il ciclo lo moltiplichiamo tante volte quanto è l’esponente e infine portiamo la variabile potenza a 1 diviso il numero generato dal ciclo.
Allego lo script completo del programma per il calcolo delle potenze con scratch.
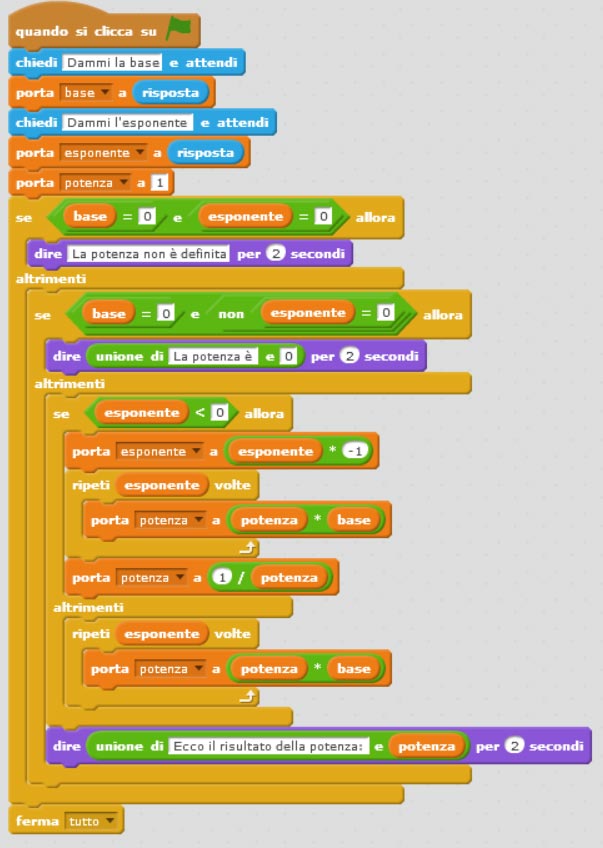
Bene e se l’esponenete fosse irrazionale?
Predisponiamo l’algoritmo che semplicemente ci avvisa che non è predisposto per il calcolo delle potenze con esponente irrazionale.
Algoritmo per calcolare la potenza con scratch nel caso in cui l’esponente è irrazionale
Realizziamo un blocco che chiameremo ad esempio controlla_intero. Quindi se ad esempio inseriamo come esponente 3.4 sarà in grado di dirmi che non è un numero intero.
Come realizziamo il blocco? Scorriamo tutto il numero con un indice i che controlla se è presente il punto da qualche parte.
In questo modo:

Adesso modifichiamo il codice di prima, inserendo semplicemente il richiamo al blocco in questo punto:
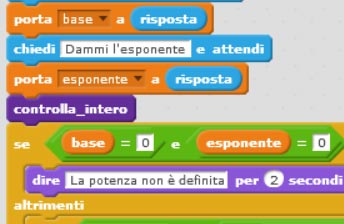
Alcuni link utili:
Sommare un intervallo di numeri con scratch
Olimpiadi di informatica con scratch
Olimpaidi di matematica con scratch
Figure equivalenti con scratch
Riconoscere gli angoli con scratch
Giochi matematici autunno 2018
Esempi di giochi matematici Bocconi
Gioco della tabellina con scratch
Gioco indovina numero con scratch
Equazioni di primo grado con scratch










Commenti recenti